Caribou
Classes | Public Types | Public Member Functions | Static Public Attributes | List of all members
caribou::geometry::Element< Derived, ScalarType > Struct Template Reference

Classes

struct  GaussNode
 

Public Types

using Scalar = ScalarType
 
template<INTEGER_TYPE Dim>
using Vector = Eigen::Matrix< Scalar, Dim, 1 >
 
template<INTEGER_TYPE Rows, INTEGER_TYPE Cols, int Options = Eigen::ColMajor>
using Matrix = Eigen::Matrix< Scalar, Rows, Cols, Options >
 
template<INTEGER_TYPE Rows, INTEGER_TYPE Cols, int Options = Eigen::ColMajor>
using MatrixI = Eigen::Matrix< Scalar, Rows, Cols, Options >
 
using LocalCoordinates = Vector< CanonicalDimension >
 
using WorldCoordinates = Vector< Dimension >
 

Public Member Functions

auto number_of_nodes () const -> UNSIGNED_INTEGER_TYPE
 Get the number of nodes in the element.
 
auto number_of_gauss_nodes () const -> UNSIGNED_INTEGER_TYPE
 Get the number of gauss nodes in the element.
 
auto node (const UNSIGNED_INTEGER_TYPE &index) const
 Get the Node at given index.
 
auto nodes () const
 Get the set of nodes.
 
auto gauss_node (const UNSIGNED_INTEGER_TYPE &index) const -> const GaussNode &
 Get the gauss node at given index.
 
auto gauss_nodes () const -> const std::vector< GaussNode > &
 Get the set of gauss nodes.
 
auto number_of_boundary_elements () const
 Get the number of boundary elements (ex. More...
 
auto boundary_elements_node_indices () const -> const auto &
 Get the list of node indices of the boundary elements. More...
 
auto boundary_element (const UNSIGNED_INTEGER_TYPE &boundary_id) const
 Construct and return the given boundary element. More...
 
auto L (const LocalCoordinates &xi) const -> Vector< NumberOfNodesAtCompileTime >
 Get the Lagrange polynomial values evaluated at local coordinates xi w.r.t each element's interpolation nodes. More...
 
auto dL (const LocalCoordinates &xi) const -> Matrix< NumberOfNodesAtCompileTime, CanonicalDimension >
 Get the Lagrange polynomial derivatives w.r.t the local frame {dL/du} evaluated at local coordinates {u} w.r.t each segment's interpolation nodes. More...
 
auto center () const -> WorldCoordinates
 Get the position at the center of the element.
 
auto world_coordinates (const LocalCoordinates &coordinates) const -> WorldCoordinates
 Get the world coordinates of a point from its local coordinates.
 
auto local_coordinates (const WorldCoordinates &coordinates) const -> LocalCoordinates
 Get the local coordinates of a point from its world coordinates by doing a set of Newton-Raphson iterations. More...
 
auto local_coordinates (const WorldCoordinates &coordinates, const LocalCoordinates &starting_point, const FLOATING_POINT_TYPE &residual_tolerance, const UNSIGNED_INTEGER_TYPE &maximum_number_of_iterations) const -> LocalCoordinates
 Get the local coordinates of a point from its world coordinates by doing a set of Newton-Raphson iterations. More...
 
auto contains_local (const LocalCoordinates &xi, const FLOATING_POINT_TYPE &eps=1e-10) const -> bool
 Return true if the element contains the point located at the given local coordinates. More...
 
template<typename MatrixType >
auto interpolate (const LocalCoordinates &coordinates, const Eigen::MatrixBase< MatrixType > &values) const
 Interpolate a value at local coordinates from the given interpolation node values. More...
 
auto jacobian (const LocalCoordinates &coordinates) const -> Matrix< Dimension, CanonicalDimension >
 Compute the Jacobian matrix of the transformation T(xi)-> x evaluated at local coordinates xi. More...
 

Static Public Attributes

static constexpr auto CanonicalDimension = traits<Derived>::CanonicalDimension
 
static constexpr auto Dimension = traits<Derived>::Dimension
 
static constexpr auto NumberOfNodesAtCompileTime = traits<Derived>::NumberOfNodesAtCompileTime
 
static constexpr auto NumberOfGaussNodesAtCompileTime = traits<Derived>::NumberOfGaussNodesAtCompileTime
 

Class Documentation

◆ caribou::geometry::Element::GaussNode

struct caribou::geometry::Element::GaussNode
Class Members
LocalCoordinates position
Scalar weight

Member Function Documentation

◆ boundary_element()

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
auto caribou::geometry::Element< Derived, ScalarType >::boundary_element ( const UNSIGNED_INTEGER_TYPE &  boundary_id) const
inline

Construct and return the given boundary element.

Example:

Hexahedron<Linear> hexa;
Quad<Linear, _3D> face_0 = hexa.boundary_element(0);
Tetrahedron<Quadratic> tetra;
Triangle<Quadratic, _3D> face_2 = tetra.boundary_element(2);

◆ boundary_elements_node_indices()

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
auto caribou::geometry::Element< Derived, ScalarType >::boundary_elements_node_indices ( ) const -> const auto &
inline

Get the list of node indices of the boundary elements.

The return type is up to the implementation but should normally be:

  1. Dynamic number of boundary element where each boundary element has a dynamic number of nodes std::vector<std::vector<unsigned int>>
  2. Dynamic number of boundary element where each boundary element has a static number of nodes std::vector<std::array<unsigned int, traits<BoundaryElement>::NumberOfNodesAtCompileTime>>
  3. Static number of boundary element where each boundary element has a dynamic number of nodes std::array<std::vector<unsigned int>, traits<Element>::NumberOfBoundaryElementsAtCompileTime>
  4. Static number of boundary element where each boundary element has a static number of nodes std::array< std::array<unsigned int, traits<BoundaryElement>::NumberOfNodesAtCompileTime>, traits<Element>::NumberOfBoundaryElementsAtCompileTime

◆ contains_local()

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
auto caribou::geometry::Element< Derived, ScalarType >::contains_local ( const LocalCoordinates &  xi,
const FLOATING_POINT_TYPE &  eps = 1e-10 
) const -> bool
inline

Return true if the element contains the point located at the given local coordinates.

Parameters
coordinatesLocal coordinates of a point
epsIf the given point is located barely outside the element, which is, less than this eps value, returns true.

◆ dL()

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
auto caribou::geometry::Element< Derived, ScalarType >::dL ( const LocalCoordinates &  xi) const -> Matrix<NumberOfNodesAtCompileTime, CanonicalDimension>
inline

Get the Lagrange polynomial derivatives w.r.t the local frame {dL/du} evaluated at local coordinates {u} w.r.t each segment's interpolation nodes.

Example:

// Computes the derivatives of node #2 Lagrange polynomial evaluated at local coordinates {-0.4}
float dp = Segment2::dL(-0.4)[2];

◆ interpolate()

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
template<typename MatrixType >
auto caribou::geometry::Element< Derived, ScalarType >::interpolate ( const LocalCoordinates &  coordinates,
const Eigen::MatrixBase< MatrixType > &  values 
) const
inline

Interpolate a value at local coordinates from the given interpolation node values.

The values at nodes must be provided in an Eigen::Matrix where the row i of the matrix is the value (as a row-vector or a scalar) at the node i.

Template Parameters
MatrixTypeType of the Eigen matrix containing the values at nodes.

◆ jacobian()

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
auto caribou::geometry::Element< Derived, ScalarType >::jacobian ( const LocalCoordinates &  coordinates) const -> Matrix<Dimension, CanonicalDimension>
inline

Compute the Jacobian matrix of the transformation T(xi)-> x evaluated at local coordinates xi.

The Jacobian is defined as:

*
* |dx|     |du|
* |dy| = J |dv|
* |dz|     |dw|
*
* 1D canonical element
* --------------------
*
* 1D manifold:    J(u) = dx/du = sum_i dNi/du * x_i
*                 det(J) = |J|
*
* 2D manifold:    J(u)  = | dx/du | = | sum dNi/du x_i |
*                         | dy/du | = | sum dNi/du y_i |
*                 det(J) = sqrt(J.dot(J))
*
*                        | dx/du | = | sum dNi/du x_i |
* 3D manifold:    J(u) = | dy/du | = | sum dNi/du y_i |
*                        | dz/du | = | sum dNi/du z_i |
*                 det(J) = sqrt(J.dot(J))
*
*
* 2D canonical element
* --------------------
*
* 1D manifold:    N/A
*
* 2D manifold:    J(u,v) = | dx/du   dx/dv |   | sum dNi/du  x_i    sum dNi/dv  x_i |
*                          | dy/du   dy/dv | = | sum dNi/du  y_i    sum dNi/dv  y_i |
*                 det(J) = |det(J)|
*
*                          | dx/du   dx/dv |   | sum dNi/du  x_i    sum dNi/dv  x_i |
* 3D manifold:    J(u,v) = | dy/du   dy/dv | = | sum dNi/du  y_i    sum dNi/dv  y_i |
*                          | dz/du   dz/dv | = | sum dNi/du  z_i    sum dNi/dv  z_i |
*                 det(J) = sqrt((J.transpose() * J).determinant())
*                        = J.col(0).cross(J.col(1)).norm();
*
*
* 3D canonical element
* --------------------
*
* 1D manifold:    N/A
* 2D manifold:    N/A
*                            | dx/du   dx/dv   dx/dw |   | sum dNi/du x_i   sum dNi/dv x_i    sum dNi/dw x_i |
* 3D manifold:    J(u,v,w) = | dy/du   dy/dv   dy/dw | = | sum dNi/du y_i   sum dNi/dv y_i    sum dNi/dw y_i |
*                            | dz/du   dz/dv   dz/dw |   | sum dNi/du z_i   sum dNi/dv z_i    sum dNi/dw z_i |
*
*
*
*
* where dNi/du (resp. dv and dw) is the partial derivative of the shape function at node i
* w.r.t the local frame of the canonical element evaluated at local coordinate  {u, v, w} and
* where {xi, yi and zi} are the world coordinates of the position of node i on its element manifold.
*

Example:

// Computes the Jacobian of a 3D segment and its determinant evaluated at local coordinates 0.5 (half-way through the segment)
Segment<3, Linear> segment {{5, 5, 5}, {10, 5,0}};
Matrix<3,1> J = segment.jacobian (0.5);
double detJ = sqrt(J.dot(J));
// Computes the Jacobian of a 3D triangle and its determinant evaluated at local coordinates {1/3, 1/3} (on its center point)
Triangle<3, Linear> triangle {{5,5,5}, {15, 5, 5}, {10, 10, 10}};
Matrix<3,2> J = triangle.jacobian(1/3., 1/3.);
double detJ = (J^T * J).determinant() ^ 1/2;
// Computes the Jacobian of a 3D tetrahedron and its determinant evaluated at local coordinates {1/3, 1/3, 1/3} (on its center point)
Tetrahedron<3> tetra {{5,5,5}, {15, 5, 5}, {10, 10, 10}};
Matrix<3,3> J = tetra.jacobian(1/3., 1/3., 1/3.);
double detJ = J.determinant();

◆ L()

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
auto caribou::geometry::Element< Derived, ScalarType >::L ( const LocalCoordinates &  xi) const -> Vector<NumberOfNodesAtCompileTime>
inline

Get the Lagrange polynomial values evaluated at local coordinates xi w.r.t each element's interpolation nodes.

Example:

// Computes the value of node #2 Lagrange polynomial evaluated at local coordinates {-0.4} on a segment
Segment<3, Linear> segment;
float p = segment.L(-0.4)[2];

◆ local_coordinates() [1/2]

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
auto caribou::geometry::Element< Derived, ScalarType >::local_coordinates ( const WorldCoordinates &  coordinates) const -> LocalCoordinates
inline

Get the local coordinates of a point from its world coordinates by doing a set of Newton-Raphson iterations.

See also
local_coordinates() for more details.
Note
By default, the Newton-Raphson will start by an approximation of the local coordinates at [0, 0, 0]. The iterations will stop at 5 iterations, or if the norm o* f relative residual |R|/|R0| is less than 1e-5.

◆ local_coordinates() [2/2]

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
auto caribou::geometry::Element< Derived, ScalarType >::local_coordinates ( const WorldCoordinates &  coordinates,
const LocalCoordinates &  starting_point,
const FLOATING_POINT_TYPE &  residual_tolerance,
const UNSIGNED_INTEGER_TYPE &  maximum_number_of_iterations 
) const -> LocalCoordinates
inline

Get the local coordinates of a point from its world coordinates by doing a set of Newton-Raphson iterations.

By taking the Taylor expansion of the transformation $T(\vec{\xi}) \rightarrow \vec{x} $ with $\vec{x} = [x,y,z]^T$ being the world coordinates of a point and $\vec{\xi} = [u,v,w]^T$ its local coordinates within the element, we have

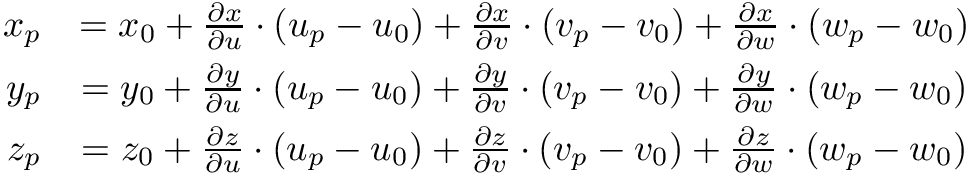
\begin{eqnarray*} x_p &= x_0 + \frac{\partial x}{\partial u} \cdot (u_p - u_0) + \frac{\partial x}{\partial v} \cdot (v_p - v_0) + \frac{\partial x}{\partial w} \cdot (w_p - w_0) \\ y_p &= y_0 + \frac{\partial y}{\partial u} \cdot (u_p - u_0) + \frac{\partial y}{\partial v} \cdot (v_p - v_0) + \frac{\partial y}{\partial w} \cdot (w_p - w_0) \\ z_p &= z_0 + \frac{\partial z}{\partial u} \cdot (u_p - u_0) + \frac{\partial z}{\partial v} \cdot (v_p - v_0) + \frac{\partial z}{\partial w} \cdot (w_p - w_0) \\ \end{eqnarray*}

where partial derivatives are evaluated at $\vec{\xi}_0 = [u_0,v_0,w_0]^T$. We can reformulate with the following matrix form

\begin{eqnarray*} \vec{x}_p = \vec{x}_0 + \mathrm{J} \cdot (\vec{\xi}_p - \vec{\xi}_0) \end{eqnarray*}

where $ \vec{x}_p = T(\vec{\xi}_p) $, $ \vec{x}_0 = T(\vec{\xi}_0) $ and $ \mathrm{J} $ is the Jacobian of the transformation $T$. Since we are trying to find $\vec{\xi}_p$, we can rearange the last equation to get

\begin{eqnarray*} \vec{\xi}_p = \vec{\xi}_0 + \mathrm{J}^{-1} (\vec{x}_p - \vec{x}_0) \end{eqnarray*}

Hence, starting from an initial guess at local coordinates $ \vec{\xi}_0 $, we have the following iterative method:

\begin{eqnarray*} \vec{\xi}_p^{k+1} = \vec{\xi}_k + \mathrm{J}^{-1} (\vec{x}_p - T(\vec{\xi}_k)) \end{eqnarray*}

The iterations stop when $ \frac{|\vec{x}_p - T(\vec{\xi}_k)|}{|\vec{x}_p - T(\vec{\xi}_0)|} < \epsilon $

Note
When trying to find the local coordinates of non-matching manifolds (for example, the local coordinates of a triangle in a 3D manifold), the following recursive formulae is used:

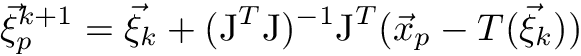
\begin{eqnarray*} \vec{\xi}_p^{k+1} = \vec{\xi}_k + (\mathrm{J}^T\mathrm{J})^{-1} \mathrm{J}^T (\vec{x}_p - T(\vec{\xi}_k)) \end{eqnarray*}

Parameters
coordinatesThe world coordinates of the point from which we want to get the local coordinates.
starting_pointAn approximation of the real local coordinates we want the get. The closer it is to the solution, the faster the Newton will converge.
residual_toleranceThe threshold of relative norm of the residual at which point the Newton is said to converge (|R|/|R0| < threshold).
maximum_number_of_iterationsThe maximum number of Newton-Raphson iterations we can do before divergence.
Returns
The local coordinates of the point at the last Newton-Raphson iteration completed.

◆ number_of_boundary_elements()

template<typename Derived , typename ScalarType = FLOATING_POINT_TYPE>
auto caribou::geometry::Element< Derived, ScalarType >::number_of_boundary_elements ( ) const
inline

Get the number of boundary elements (ex.

number of triangles in a tetrahedron)

The documentation for this struct was generated from the following file:
Generated by doxygen 1.8.20